by Prof. Fabrice Laussy, Consejo Superior de Investigaciones Científicas
In HEISINGBERG, the phases of pixels from a spatial light modulator (SLM) are used to encode the states of digital spins that simulate a physical system. The project extends the scheme developed by the Sapienza node [1] in various directions and dimensions, from simply making it faster, bigger, more accurate and more efficient, to encoding more complicated systems and developing new classes of algorithms.
One of the exciting conceptual leap forward is to go quantum. So far, the machine is classical as it operates with coherent states of light. One goal of HEISINGBERG is to upgrade from classical to quantum light, and thus put a foot in one of the most actively pursued technological resource: quantum information processing.
Quantum light is considerably richer than classical light, which is basically an amplitude and a phase (and some fluctuations in more advanced, yet still classical treatments). In terms of power, potential and complexity, quantum light is to classical light what a modern supercomputer is to the abacus. There is therefore a lot for the HEISINGBERG consortium to investigate, try, discover and, ultimately, turn into new technological applications.
Quantum light is also, for the same reasons, much more complicated to deal with. Both its manipulation, processing and detection present considerable challenges. A first approach to the formidable problem of bringing quantum features to a spin photonic machine, is to rely on the simplest type of quantum light, namely, Gaussian states of light. This includes the coherent state itself, but this time with a strict adherence to the Heisenberg uncertainties in terms of the accuracy with which intensity and phase can be jointly defined. In the classical treatment, they can be both perfectly determined. In quantum mechanics, however, there is an inherent noise in those observables. A popular class of Gaussian states—the so-called squeezed states—have been studied and produced in the 80s, precisely for their ability to squeeze the noise of one observable, into another, say, to make the phase uncertainty smaller, at the detriment of the intensity uncertainty. Given the privileged role of the phase in an SLM, such a possibility could already endow our machine with super-classical attributes. This was, for instance, crucial for the LIGO interferometer, which could operate only by beating the standard quantum limit.
Squeezing brings another great potential for HEISINGBERG. Namely, at the two-photon level—which is the starting point of any quantum optical experiment—admixtures of squeezing and coherent states are basically as good as non-Gaussian (more strongly quantum correlated) light anyway [2]. By controlling the relative phase between an interfering coherent and squeezed state, one can produce the full range of correlations from single-photon emission (known as antibunching) to all-order multiphoton emission (superbunching) [3]. A SLM is an ideal device to study such phase control of the quantum correlations of Gaussian state admixtures.
In its full operating regime, the HEISINGBERG machine will proceed with readout and iterations. In a first stage, however, before operating each of the several thousand pixels in its role of simulating a logical spin, one has to understand, characterize and control more basic effects, including the quantum state of the driving light itself, how it interacts with the SLM and what type of quantum measurements can be made at the output. Typical quantum-optical measurements involve correlations. HEISINGBERG provides us with a platform to correlate both in space and time. This already provides us with exciting prospects, such as revisiting the wave-particle duality, turning our SLM into a multi-port interferometer, observing bosonic quantum correlations in space and thus making a multiphoton spatial HOM experiment, tuning quantum correlations by phase modulation, etc., among a long list of fundamental quantum optical effects which can be upscaled considerably thanks to the technology developed by our consortium. Before we let a Metropolis algorithm crunch our pixels to track the ground state of some Hamiltonian, a major goal of the Quantum team is to demonstrate quantum optical effects revisited through the SLM. In such attempts, we aim to demonstrate that the phase is a powerful, if not universal key to tailor quantum correlations.
A bit like CERN graced the world with the Internet in its search for the Higgs boson, it is likely, almost compulsory, that HEISINGBERG will also enlighten us on the most fundamental workings of quantum mechanics, in our pursuit of making the best optical spin machines.
[1] D. Pierangeli, G. Marcucci, and C. Conti. Large-scale photonic Ising machine by spatial light modulation. Phys. Rev. Lett., 122:213902, 2019. [ http://dx.doi.org/10.1103/PhysRevLett.122.213902 ]
[2] E. Zubizarreta Casalengua, F. P. Laussy, and E. del Valle. Two photons everywhere. Phil. Trans. R. Soc. Lond. A, 382:20230315, 2024. [ http://dx.doi.org/10.1098/rsta.2023.0315 ]
[3] E. Zubizarreta Casalengua, J. C. López Carreño, F. P. Laussy, and E. del Valle. Tuning photon statistics with coherent fields. Phys. Rev. A, 101:063824, 2020. [http://dx.doi.org/10.1103/PhysRevA.101.063824 ]
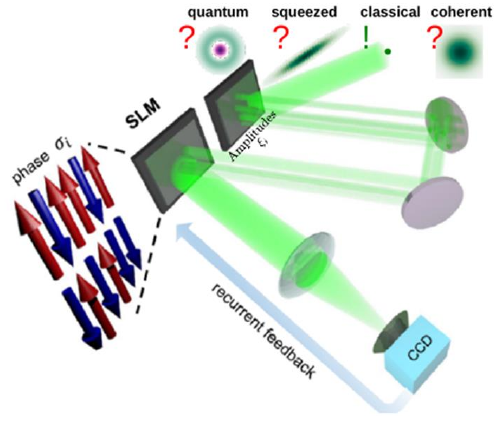
The HEISINGBERG machine: spins are encoded through the phase on pixels of a SLM. So far the machine operates with classical light, which is theoretically a point in phase space. Gaussian states, such as coherent and squeezed states, would bring the machine beyond a purely classical picture. Admixtures of Gaussian states can realize quantum states and imbue the machines with nontrivial multiphoton correlations. Studying the phase-control at the pixel level of interfering quantum states—from excitation, processing and down to detection—is the first major objective of the Quantum team of the HEISINGBERG consortium.
